摘要
JDK:1.8.0_202
# 一:前言
根据时间复杂度的不同,主流的排序算法可以分为3大类。
- 时间复杂度为O(n2)的排序算法
- 冒泡排序
- 选择排序
- 插入排序
- 希尔排序(希尔排序比较特殊,它的性能略优于O(n2),但又比不上O(nlogn),姑且把它归入本类)
- 时间复杂度为O(nlogn)的排序算法
- 快速排序
- 归并排序
- 堆排序
- 时间复杂度为线性的排序算法
- 计数排序
- 桶排序
- 基数排序
以上列举的只是最主流的排序算法
即如果值相同的元素在排序后仍然保持着排序前的顺序,则这样的排序算法是稳定排序;如果值相同的元素在排序后打乱了排序前的顺序,则这样的排序算法是不稳定排序。例如下面的例子。

在大多数场景中,值相同的元素谁先谁后是无所谓的。但是在某些场景下,值相同的元素必须保持原有的顺序。
# 二:冒泡排序
# 2.1 冒泡排序
冒泡排序之所以叫冒泡排序,因为这种排序算法的每一个元素都可以像小气泡一样,根据自身大小,一点一点地向着数组的一侧移动。冒泡排序是一种稳定排序,值相等的元素并不会打乱原本的顺序。由于该排序算法的每一轮都要遍历所有元素,总共遍历(元素数量-1)轮,所以平均时间复杂度是O(n2)。
第一版代码:
public class BubbleSort {
public static void sort(int[] array) {
for (int i = 0; i < array.length - 1; i++) {
for (int j = 0; j < array.length - i - 1; j++) {
int tmp = 0;
if (array[j] > array[j + 1]) {
tmp = array[j];
array[j] = array[j + 1];
array[j + 1] = tmp;
}
}
}
}
public static void main(String[] args) {
int[] array = new int[]{5, 8, 6, 3, 9, 2, 1, 7};
sort(array);
System.out.println(Arrays.toString(array)); // [1, 2, 3, 5, 6, 7, 8, 9]
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
缺点:上面代码执行次数一定是 n-1,但有可能前面几轮就已经排好序了,这样后面的几次遍历排序没必要执行了。
第二版代码:
public class BubbleSort {
public static void sort(int[] array) {
for (int i = 0; i < array.length - 1; i++) {
//有序标记,每一轮的初始值都是true
boolean isSorted = true;
for (int j = 0; j < array.length - i - 1; j++) {
int tmp = 0;
if (array[j] > array[j + 1]) {
tmp = array[j];
array[j] = array[j + 1];
array[j + 1] = tmp;
//因为有元素进行交换,所以不是有序的,标记变为false
isSorted = false;
}
}
if (isSorted) {
break;
}
}
}
public static void main(String[] args) {
int[] array = new int[]{5, 8, 6, 3, 9, 2, 1, 7};
sort(array);
System.out.println(Arrays.toString(array)); // [1, 2, 3, 5, 6, 7, 8, 9]
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
与第1版代码相比,第2版代码做了小小的改动,利用布尔变量isSorted作为标记。如果在本轮排序中,元素有交换,则说明数列无序;如果没有元素交换,则说明数列已然有序,然后直接跳出大循环。
缺点:例如:3,4,2,1,5,6,7,8,右面的许多元素已经是有序的了,可是每一轮还是白白地比较了许多次。这个问题的关键点在于对数列有序区的界定。
按照现有的逻辑,有序区的长度和排序的轮数是相等的。例如第1轮排序过后的有序区长度是1,第2轮排序过后的有序区长度是2 ……
实际上,数列真正的有序区可能会大于这个长度,如上述例子中在第2轮排序时,后面的5个元素实际上都已经属于有序区了。因此后面的多次元素比较是没有意义的。
那么,该如何避免这种情况呢?可以在每一轮排序后,记录下来最后一次元素交换的位置,该位置即为无序数列的边界,再往后就是有序区了。
第三版代码:
public class BubbleSort {
public static void sort(int[] array) {
//记录最后一次交换的位置
int lastExchangeIndex = 0;
//无序数列的边界,每次比较只需要比到这里为止
int sortBorder = array.length - 1;
for (int i = 0; i < array.length - 1; i++) {
//有序标记,每一轮的初始值都是true
boolean isSorted = true;
for (int j = 0; j < sortBorder; j++) {
int tmp = 0;
if (array[j] > array[j + 1]) {
tmp = array[j];
array[j] = array[j + 1];
array[j + 1] = tmp;
// 因为有元素进行交换,所以不是有序的,标记变为false
isSorted = false;
// 更新为最后一次交换元素的位置
lastExchangeIndex = j;
}
}
sortBorder = lastExchangeIndex;
if (isSorted) {
break;
}
}
}
public static void main(String[] args) {
int[] array = new int[]{3, 4, 2, 1, 5, 6, 7, 8};
sort(array);
System.out.println(Arrays.toString(array)); // [1, 2, 3, 4, 5, 6, 7, 8]
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
sortBorder就是无序数列的边界。在每一轮排序过程中,处于sortBorder之后的元素就不需要再进行比较了,肯定是有序的。
# 2.2 鸡尾酒排序
基于冒泡排序的一种升级排序法。鸡尾酒排序的元素比较和交换过程是双向的。
例子:2,3,4,5,6,7,8,1
如果按照冒泡排序的思想,排序过程如下:

缺点:元素2、3、4、5、6、7、8已经是有序的了,只有元素1的位置不对,却还要进行7轮排序!
鸡尾酒排序过程如下:
第1轮(和冒泡排序一样,8和1交换)

此时开始不一样了,反过来从右往左比较并进行交换。

第3轮(虽然实际上已经有序,但是流程并没有结束)
在鸡尾酒排序的第3轮,需要重新从左向右比较并进行交换。
1和2比较,位置不变;2和3比较,位置不变;3和4比较,位置不变……6和7比较,位置不变。
没有元素位置进行交换,证明已经有序,排序结束。
这就是鸡尾酒排序的思路。排序过程就像钟摆一样,第1轮从左到右,第2轮从右到左,第3轮再从左到右……
代码实现:
public class CocktailSort {
public static void sort(int array[]) {
int tmp = 0;
for (int i = 0; i < array.length / 2; i++) {
//有序标记,每一轮的初始值都是true
boolean isSorted = true;
//奇数轮,从左向右比较和交换
for (int j = i; j < array.length - i - 1; j++) {
if (array[j] > array[j + 1]) {
tmp = array[j];
array[j] = array[j + 1];
array[j + 1] = tmp;
// 有元素交换,所以不是有序的,标记变为false
isSorted = false;
}
}
if (isSorted) {
break;
}
// 在偶数轮之前,将isSorted重新标记为true
isSorted = true;
//偶数轮,从右向左比较和交换
for (int j = array.length - i - 1; j > i; j--) {
if (array[j] < array[j - 1]) {
tmp = array[j];
array[j] = array[j - 1];
array[j - 1] = tmp;
// 因为有元素进行交换,所以不是有序的,标记变为false
isSorted = false;
}
}
if (isSorted) {
break;
}
}
}
public static void main(String[] args) {
int[] array = new int[]{2, 3, 4, 5, 6, 7, 8, 1};
sort(array);
System.out.println(Arrays.toString(array)); // [1, 2, 3, 4, 5, 6, 7, 8]
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
鸡尾酒排序的优点是能够在特定条件下(大部分元素已经有序的情况),减少排序的回合数;而缺点也很明显,就是代码量几乎增加了1倍。
# 三:快速排序
同冒泡排序一样,快速排序也属于交换排序,通过元素之间的比较和交换位置来达到排序的目的。
不同的是,冒泡排序在每一轮中只把1个元素冒泡到数列的一端,而快速排序则在每一轮挑选一个基准元素,并让其他比它大的元素移动到数列一边,比它小的元素移动到数列的另一边,从而把数列拆解成两个部分。
这种思路就叫作分治法。
而快速排序的流程是什么样子呢?
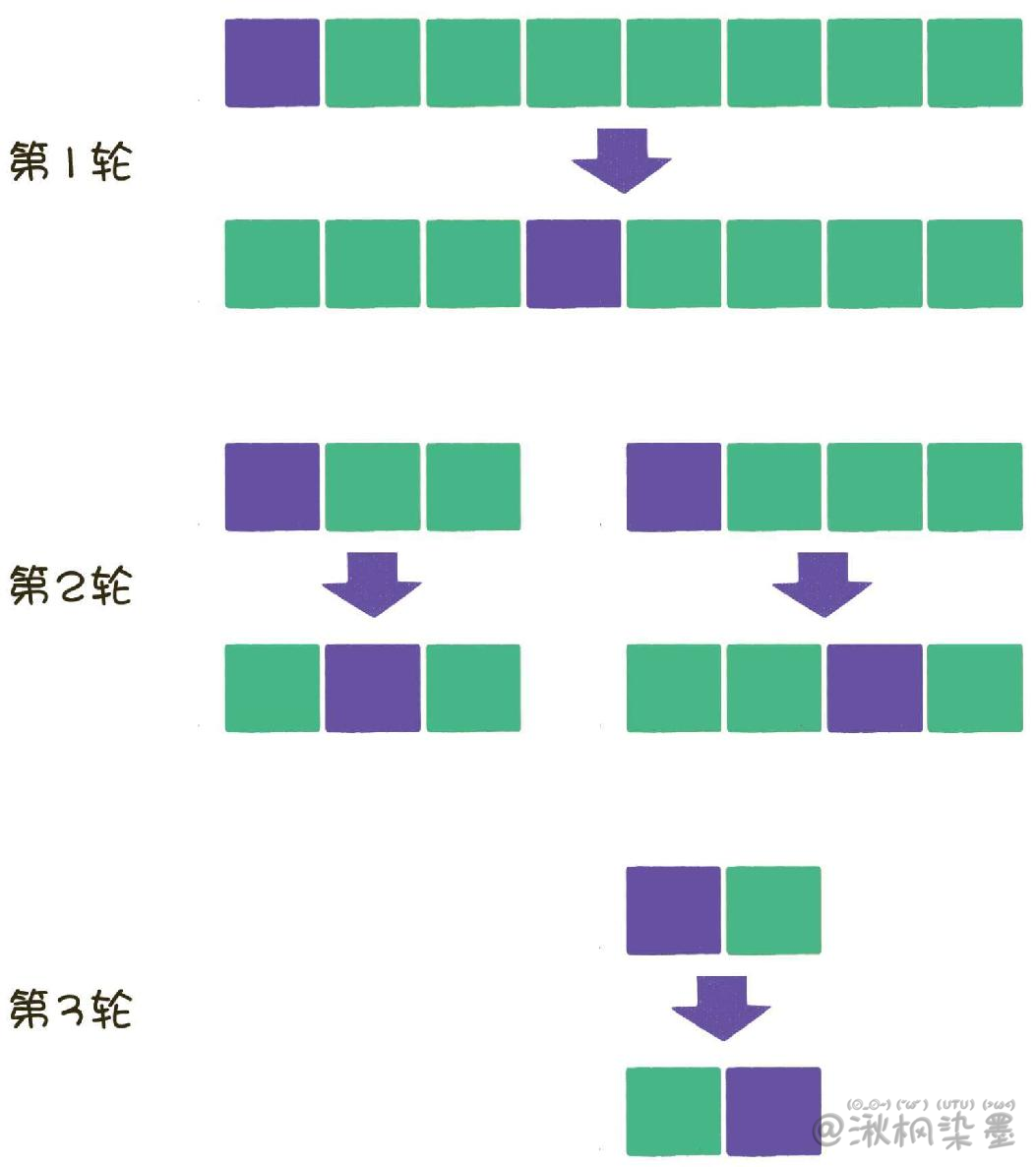
如图所示,在分治法的思想下,原数列在每一轮都被拆分成两部分,每一部分在下一轮又分别被拆分成两部分,直到不可再分为止。
每一轮的比较和交换,需要把数组全部元素都遍历一遍,时间复杂度是O(n)。这样的遍历一共需要多少轮呢?假如元素个数是n,那么平均情况下需要logn轮,因此快速排序算法总体的平均时间复杂度是O(nlogn)。
# 3.1 基准元素的选择
基准元素(pivot),在分治过程中,以基准元素为中心,把其他元素移动到它的左右两边。
Q:那么如何选择基准元素呢?
最简单的方式是选择数列的第1个元素。这种选择在绝大多数情况下是没有问题的。但如果数列的第1个元素要么是最小值,要么是最大值,根本无法发挥分治法的优势。在这种极端情况下,快速排序需要进行n轮,时间复杂度退化成了O(n2)。这种情况下,可以随机选择一个元素作为基准元素,并且让基准元素和数列首元素交换位置。这样一来,即使在数列完全逆序的情况下,也可以有效地将数列分成两部分。当然,即使是随机选择基准元素,也会有极小的几率选到数列的最大值或最小值,同样会影响分治的效果。所以,虽然快速排序的平均时间复杂度是O(nlogn),但最坏情况下的时间复杂度是O(n2)。
# 3.2 元素交换
有两种方法:
- 双边循环法;
- 单边循环法。
双边循环法:
给出原始数列如下,要求对其从小到大进行排序。

首先,选定基准元素pivot,并且设置两个指针left和right,指向数列的最左和最右两个元素。

接下来进行第1次循环,从right指针开始,让指针所指向的元素和基准元素做比较。如果大于或等于pivot,则指针向左移动;如果小于pivot,则right指针停止移动,切换到left指针。
在当前数列中,1<4,所以right直接停止移动,换到left指针,进行下一步行动。
轮到left指针行动,让指针所指向的元素和基准元素做比较。如果小于或等于pivot,则指针向右移动;如果大于pivot,则left指针停止移动。
由于left开始指向的是基准元素,判断肯定相等,所以left右移1位。

由于7>4,left指针在元素7的位置停下。这时,让left和right指针所指向的元素进行交换。

接下来,进入第2次循环,重新切换到right指针,向左移动。right指针先移动到8,8>4,继续左移。由于2<4,停止在2的位置。
按照这个思路,后续步骤如图所示。

代码实现:(递归)
public class QuickSort1 {
public static void quickSort(int[] arr, int startIndex, int endIndex) {
// 递归结束条件:startIndex大于或等于endIndex时
if (startIndex >= endIndex) {
return;
}
// 得到基准元素位置
int pivotIndex = partition(arr, startIndex, endIndex);
// 根据基准元素,分成两部分进行递归排序
quickSort(arr, startIndex, pivotIndex - 1);
quickSort(arr, pivotIndex + 1, endIndex);
}
/**
* 分治(双边循环法)
*
* @param arr 待交换的数组
* @param startIndex 起始下标
* @param endIndex 结束下标
*/
private static int partition(int[] arr, int startIndex, int endIndex) {
// 取第1个位置(也可以选择随机位置)的元素作为基准元素
int pivot = arr[startIndex];
int left = startIndex;
int right = endIndex;
while (left != right) {
//控制right 指针比较并左移
while (left < right && arr[right] > pivot) {
right--;
}
//控制left指针比较并右移
while (left < right && arr[left] <= pivot) {
left++;
}
//交换left和right 指针所指向的元素
if (left < right) {
int p = arr[left];
arr[left] = arr[right];
arr[right] = p;
}
}
//pivot 和指针重合点交换
arr[startIndex] = arr[left];
arr[left] = pivot;
return left;
}
public static void main(String[] args) {
int[] arr = new int[]{4, 4, 6, 5, 3, 2, 8, 1};
quickSort(arr, 0, arr.length - 1);
System.out.println(Arrays.toString(arr)); // [1, 2, 3, 4, 4, 5, 6, 8]
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
单边循环法
给出原始数列如下,要求对其从小到大进行排序。

开始和双边循环法相似,首先选定基准元素pivot。同时,设置一个mark指针指向数列起始位置,这个mark指针代表小于基准元素的区域边界。

接下来,从基准元素的下一个位置开始遍历数组。
如果遍历到的元素大于基准元素,就继续往后遍历。
如果遍历到的元素小于基准元素,则需要做两件事:第一,把mark指针右移1位,因为小于pivot的区域边界增大了1;第二,让最新遍历到的元素和mark指针所在位置的元素交换位置,因为最新遍历的元素归属于小于pivot的区域。
首先遍历到元素7,7>4,所以继续遍历。

接下来遍历到的元素是3,3<4,所以mark指针右移1位。

随后,让元素3和mark指针所在位置的元素交换,因为元素3归属于小于pivot的区域。

按照这个思路,继续遍历,后续步骤如图所示。
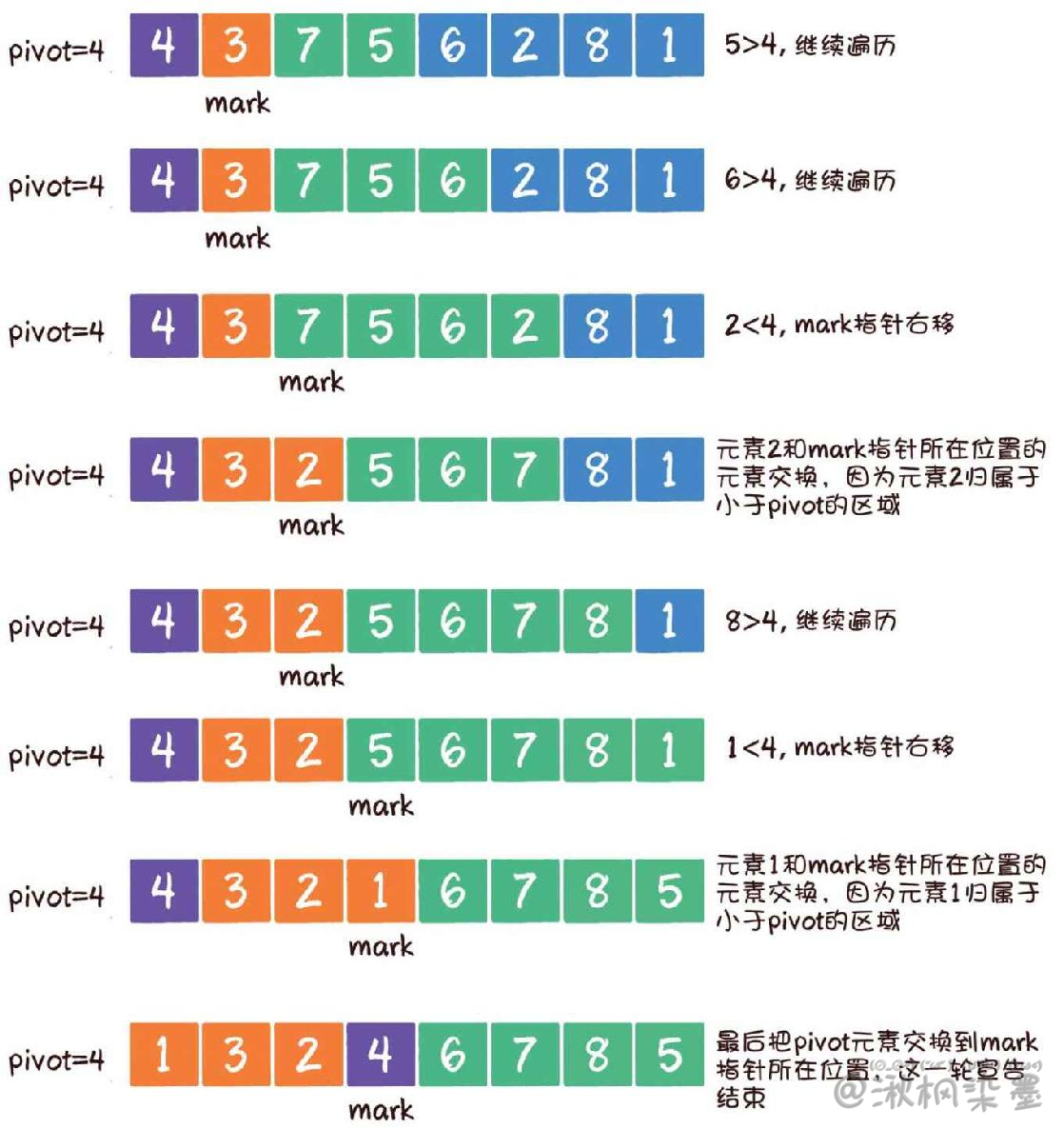
代码实现:(递归)
public class QuickSort2 {
public static void quickSort(int[] arr, int startIndex, int endIndex) {
// 递归结束条件:startIndex大于或等于endIndex时
if (startIndex >= endIndex) {
return;
}
// 得到基准元素位置
int pivotIndex = partition(arr, startIndex, endIndex);
// 根据基准元素,分成两部分进行递归排序
quickSort(arr, startIndex, pivotIndex - 1);
quickSort(arr, pivotIndex + 1, endIndex);
}
/**
* 分治(单边循环法)
*
* @param arr 待交换的数组
* @param startIndex 起始下标
* @param endIndex 结束下标
*/
private static int partition(int[] arr, int startIndex, int endIndex) {
// 取第1个位置(也可以选择随机位置)的元素作为基准元素
int pivot = arr[startIndex];
int mark = startIndex;
for (int i = startIndex + 1; i <= endIndex; i++) {
if (arr[i] < pivot) {
mark++;
int p = arr[mark];
arr[mark] = arr[i];
arr[i] = p;
}
}
arr[startIndex] = arr[mark];
arr[mark] = pivot;
return mark;
}
public static void main(String[] args) {
int[] arr = new int[]{4, 4, 6, 5, 3, 2, 8, 1};
quickSort(arr, 0, arr.length - 1);
System.out.println(Arrays.toString(arr)); // [1, 2, 3, 4, 4, 5, 6, 8]
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
# 3.3 代码非递归实现
绝大多数的递归逻辑,都可以用栈的方式来代替。代码中一层一层的方法调用,本身就使用了一个方法调用栈。每次进入一个新方法,就相当于入栈;每次有方法返回,就相当于出栈。
所以,可以把原本的递归实现转化成一个栈的实现,在栈中存储每一次方法调用的参数。

public class QuickSort3 {
public static void quickSort(int[] arr, int startIndex, int endIndex) {
// 用一个集合栈来代替递归的函数栈
Stack<Map<String, Integer>> quickSortStack = new Stack<>();
// 整个数列的起止下标,以哈希的形式入栈
Map<String, Integer> rootParam = new HashMap<>();
rootParam.put("startIndex", startIndex);
rootParam.put("endIndex", endIndex);
quickSortStack.push(rootParam);
// 循环结束条件:栈为空时
while (!quickSortStack.isEmpty()) {
// 栈顶元素出栈,得到起止下标
Map<String, Integer> param = quickSortStack.pop();
// 得到基准元素位置
int pivotIndex = partition(arr, param.get("startIndex"), param.get("endIndex"));
// 根据基准元素分成两部分, 把每一部分的起止下标入栈
if (param.get("startIndex") < pivotIndex - 1) {
Map<String, Integer> leftParam = new HashMap<String, Integer>();
leftParam.put("startIndex", param.get("startIndex"));
leftParam.put("endIndex", pivotIndex - 1);
quickSortStack.push(leftParam);
}
if (pivotIndex + 1 < param.get("endIndex")) {
Map<String, Integer> rightParam = new HashMap<String, Integer>();
rightParam.put("startIndex", pivotIndex + 1);
rightParam.put("endIndex", param.get("endIndex"));
quickSortStack.push(rightParam);
}
}
}
/**
* 分治(单边循环法)
*
* @param arr 待交换的数组
* @param startIndex 起始下标
* @param endIndex 结束下标
*/
private static int partition(int[] arr, int startIndex, int endIndex) {
// 取第1个位置(也可以选择随机位置)的元素作为基准元素
int pivot = arr[startIndex];
int mark = startIndex;
for (int i = startIndex + 1; i <= endIndex; i++) {
if (arr[i] < pivot) {
mark++;
int p = arr[mark];
arr[mark] = arr[i];
arr[i] = p;
}
}
arr[startIndex] = arr[mark];
arr[mark] = pivot;
return mark;
}
public static void main(String[] args) {
int[] arr = new int[]{4, 7, 6, 5, 3, 2, 8, 1};
quickSort(arr, 0, arr.length - 1);
System.out.println(Arrays.toString(arr)); // [1, 2, 3, 4, 5, 6, 7, 8]
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
和刚才的递归实现相比,非递归方式代码的变动只发生在quickSort方法中。该方法引入了一个存储Map类型元素的栈,用于存储每一次交换时的起始下标和结束下标。
每一次循环,都会让栈顶元素出栈,通过partition方法进行分治,并且按照基准元素的位置分成左右两部分,左右两部分再分别入栈。当栈为空时,说明排序已经完毕,退出循环。
# 四:堆排序
以最大堆为例,如果删除一个最大堆的堆顶(并不是完全删除,而是跟末尾的节点交换位置),经过自我调整,第2大的元素就会被交换上来,成为最大堆的新堆顶。反复操作,原本的最大二叉堆会变成了一个从小到大的有序集合。
第一次:
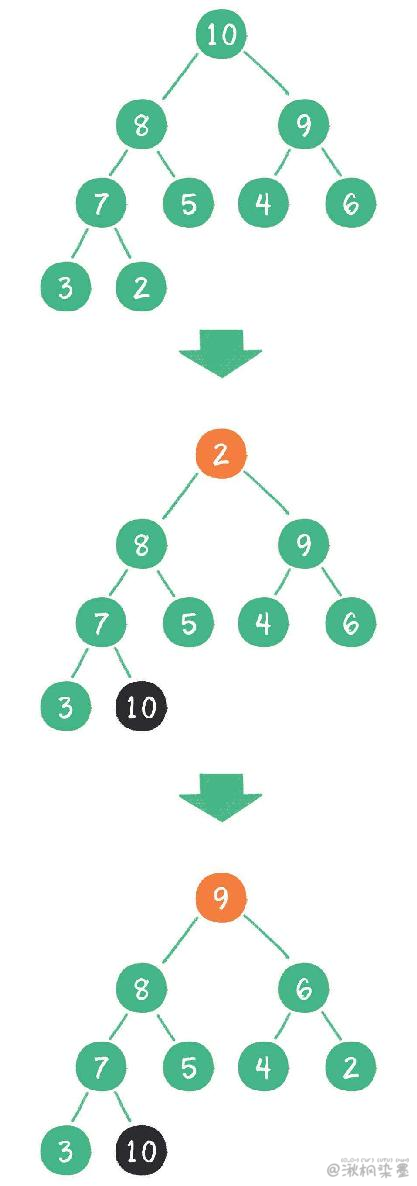
第八次:

如果此时把二叉堆实际存储在数组中,数组中的元素排列如下:

由此,可以归纳出堆排序算法的步骤:
- 把无序数组构建成二叉堆。需要从小到大排序,则构建成最大堆;需要从大到小排序,则构建成最小堆;
- 循环删除堆顶元素,替换到二叉堆的末尾,调整堆产生新的堆顶。
代码实现:
public class HeapSort {
/**
* "下沉"调整
*
* @param array 待调整的堆
* @param parentIndex 要"下沉"的父节点
* @param length 堆的有效大小
*/
public static void downAdjust(int[] array, int parentIndex, int length) {
// temp 保存父节点值,用于最后的赋值
int temp = array[parentIndex];
int childIndex = 2 * parentIndex + 1;
while (childIndex < length) {
// 如果有右孩子,且右孩子大于左孩子的值,则定位到右孩子
if (childIndex + 1 < length && array[childIndex + 1] > array[childIndex]) {
childIndex++;
}
// 如果父节点大于任何一个孩子的值,则直接跳出
if (temp >= array[childIndex]) break;
//无须真正交换,单向赋值即可
array[parentIndex] = array[childIndex];
parentIndex = childIndex;
childIndex = 2 * childIndex + 1;
}
array[parentIndex] = temp;
}
/**
* 堆排序(升序)
*
* @param array 待调整的堆
*/
public static void heapSort(int[] array) {
// 把无序数组构建成最大堆
for (int i = (array.length - 2) / 2; i >= 0; i--) {
downAdjust(array, i, array.length);
}
System.out.println(Arrays.toString(array));
// 循环删除堆顶元素,移到集合尾部,调整堆产生新的堆顶
for (int i = array.length - 1; i > 0; i--) {
// 最后1个元素和第1个元素进行交换
int temp = array[i];
array[i] = array[0];
array[0] = temp;
// "下沉"调整最大堆
downAdjust(array, 0, i);
}
}
public static void main(String[] args) {
int[] arr = new int[]{1, 3, 2, 6, 5, 7, 8, 9, 10, 0};
heapSort(arr); // [10, 9, 8, 6, 5, 7, 2, 3, 1, 0]
System.out.println(Arrays.toString(arr)); // [0, 1, 2, 3, 5, 6, 7, 8, 9, 10]
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
# 五:计数排序
有一些特殊的排序并不基于元素比较,如计数排序、桶排序、基数排序。以计数排序来说,这种排序算法是利用数组下标来确定元素的正确位置的。
假设数组中有20个随机整数,取值范围为0~10,要求用最快的速度把这20个整数从小到大进行排序。
考虑到这些整数只能够在0、1、2、3、4、5、6、7、8、9、10这11个数中取值,取值范围有限。所以,可以根据这有限的范围,建立一个长度为11的数组。数组下标从0到10,元素初始值全为0。

假设20个随机整数的值为:9,3,5,4,9,1,2,7,8,1,3,6,5,3,4,0,10,9 ,7,9
下面就开始遍历这个无序的随机数列,每一个整数按照其值对号入座,同时,对应数组下标的元素进行加1操作。
例如第1个整数是9,那么数组下标为9的元素加1。

第2个整数是3,那么数组下标为3的元素加1。

继续遍历数列并修改数组… …
最终,当数列遍历完毕时,数组的状态如下。

该数组中每一个下标位置的值代表数列中对应整数出现的次数。
有了这个统计结果,排序就很简单了。直接遍历数组,输出数组元素的下标值,元素的值是几,就输出几次。0,1,1,2,3,3,3,4,4,5,5,6,7,7,8,9,9,9,9,10
这就是计数排序的基本过程,它适用于一定范围内的整数排序。在取值范围不是很大的情况下,它的性能甚至快过那些时间复杂度为O(nlogn)的排序。
# 5.1 代码实现
第一版:
public class CountSort {
public static int[] countSort(int[] array) {
//得到数列的最大值
int max = array[0];
for (int i = 1; i < array.length; i++) {
if (array[i] > max) {
max = array[i];
}
}
//根据数列最大值确定统计数组的长度
int[] countArray = new int[max + 1];
//遍历数列,填充统计数组
for (int i = 0; i < array.length; i++) {
countArray[array[i]]++;
}
//遍历统计数组,输出结果
int index = 0;
int[] sortedArray = new int[array.length];
for (int i = 0; i < countArray.length; i++) {
for (int j = 0; j < countArray[i]; j++) {
sortedArray[index++] = i;
}
}
return sortedArray;
}
public static void main(String[] args) {
int[] array = new int[]{4, 4, 6, 5, 3, 2, 8, 1, 7, 5, 6, 0, 10};
int[] sortedArray = countSort(array);
System.out.println(Arrays.toString(sortedArray)); // [0, 1, 2, 3, 4, 4, 5, 5, 6, 6, 7, 8, 10]
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
这段代码在开头有一个步骤,就是求数列的最大整数值max。后面创建的统计数组countArray,长度是max+1,以此来保证数组的最后一个下标是max。
缺点:
- 只以数列的最大值来决定统计数组的长度,其实并不严谨,例如
95,94,91,98,99,90,99,93,91,92这样会造成0到89空间位置浪费。
解决方法:只要不再以输入数列的最大值+1作为统计数组的长度,而是以数列最大值-最小值+1作为统计数组的长度即可。同时,数列的最小值作为一个偏移量,用于计算整数在统计数组中的下标。以刚才的数列为例,统计出数组的长度为99-90+1=10,偏移量等于数列的最小值90。对于第1个整数95,对应的统计数组下标是95-90 = 5。
- 只是简单地按照统计数组的下标输出元素值,并没有真正给原始数列进行排序。例如,下面这种情况。

给出一个学生成绩表,要求按成绩从低到高进行排序,如果成绩相同,则遵循原表固有顺序。
那么,当我们填充统计数组以后,只知道有两个成绩并列为95分的同学,却不知道哪一个是小红,哪一个是小绿。

解决方法:将之前的统计数组变形成下面的样子。

这是如何变形的呢?其实就是从统计数组的第2个元素开始,每一个元素都加上前面所有元素之和。
这样相加的目的,是让统计数组存储的元素值,等于相应整数的最终排序位置的序号。例如下标是9的元素值为5,代表原始数列的整数9,最终的排序在第5位。
接下来,创建输出数组sortedArray,长度和输入数列一致。然后从后向前遍历输入数列。
第1步,遍历成绩表最后一行的小绿同学的成绩。
小绿的成绩是95分,找到countArray下标是5的元素,值是4,代表小绿的成绩排名位置在第4位。
同时,给countArray下标是5的元素值减1,从4变成3,代表下次再遇到95分的成绩时,最终排名是第3。

第2步,遍历成绩表倒数第2行的小白同学的成绩。
小白的成绩是94分,找到countArray下标是4的元素,值是2,代表小白的成绩排名位置在第2位。
同时,给countArray下标是4的元素值减1,从2变成1,代表下次再遇到94分的成绩时(实际上已经遇不到了),最终排名是第1。

第3步,遍历成绩表倒数第3行的小红同学的成绩。
小红的成绩是95分,找到countArray下标是5的元素,值是3(最初是4,减1变成了3),代表小红的成绩排名位置在第3位。
同时,给countArray下标是5的元素值减1,从3变成2,代表下次再遇到95分的成绩时(实际上已经遇不到了),最终排名是第2。

这样一来,同样是95分的小红和小绿就能够清楚地排出顺序了,也正因为此,优化版本的计数排序属于稳定排序。
第二版:
public class CountSort {
public static int[] countSort(int[] array) {
//得到数列的最大值和最小值,并算出差值d
int max = array[0];
int min = array[0];
for (int i = 1; i < array.length; i++) {
if (array[i] > max) {
max = array[i];
}
if (array[i] < min) {
min = array[i];
}
}
int d = max - min;
//创建统计数组并统计对应元素的个数
int[] countArray = new int[d + 1];
for (int i = 0; i < array.length; i++) {
countArray[array[i] - min]++;
}
//统计数组做变形,后面的元素等于前面的元素之和
for (int i = 1; i < countArray.length; i++) {
countArray[i] += countArray[i - 1];
}
//倒序遍历原始数列,从统计数组找到正确位置,输出到结果数组
int[] sortedArray = new int[array.length];
for (int i = array.length - 1; i >= 0; i--) {
sortedArray[countArray[array[i] - min] - 1] = array[i];
countArray[array[i] - min]--;
}
return sortedArray;
}
public static void main(String[] args) {
int[] array = new int[]{95, 94, 91, 98, 99, 90, 99, 93, 91, 92};
int[] sortedArray = countSort(array);
System.out.println(Arrays.toString(sortedArray)); // [90, 91, 91, 92, 93, 94, 95, 98, 99, 99]
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
# 5.2 局限性
- 当数列最大和最小值差距过大时,并不适合用计数排序;
- 当数列元素不是整数时,也不适合用计数排序。
对于这些局限性,另一种线性时间排序算法做出了弥补,这种排序算法叫作桶排序。
# 六:桶排序
桶排序同样是一种线性时间的排序算法。类似于计数排序所创建的统计数组,桶排序需要创建若干个桶来协助排序。所谓的 "桶"(bucket)就是代表一个区间范围,里面可以承载一个或多个元素。
假设有一个非整数数列如下:4.5,0.84,3.25,2.18,0.5
桶排序的第1步,就是创建这些桶,并确定每一个桶的区间范围。

具体需要建立多少个桶,如何确定桶的区间范围,有很多种不同的方式。我们这里创建的桶数量等于原始数列的元素数量,除最后一个桶只包含数列最大值外,前面各个桶的区间按照比例来确定。
区间跨度 = (最大值-最小值)/ (桶的数量 - 1)
第2步,遍历原始数列,把元素对号入座放入各个桶中。

第3步,对每个桶内部的元素分别进行排序(显然,只有第1个桶需要排序)。

第4步,遍历所有的桶,输出所有元素。
0.5,0.84,2.18,3.25,4.5
# 6.1 代码实现
public class BucketSort {
public static double[] bucketSort(double[] array) {
//得到数列的最大值和最小值,并算出差值d
double max = array[0];
double min = array[0];
for (int i = 1; i < array.length; i++) {
if (array[i] > max) {
max = array[i];
}
if (array[i] < min) {
min = array[i];
}
}
double d = max - min;
//初始化桶
int bucketNum = array.length;
ArrayList<LinkedList<Double>> bucketList = new ArrayList<>(bucketNum);
for (int i = 0; i < bucketNum; i++) {
bucketList.add(new LinkedList<>());
}
//遍历原始数组,将每个元素放入桶中
for (int i = 0; i < array.length; i++) {
int num = (int) ((array[i] - min) * (bucketNum - 1) / d);
bucketList.get(num).add(array[i]);
}
//对每个桶内部进行排序
for (int i = 0; i < bucketList.size(); i++) {
//JDK 底层采用了归并排序或归并的优化版本
Collections.sort(bucketList.get(i));
}
//输出全部元素
double[] sortedArray = new double[array.length];
int index = 0;
for (LinkedList<Double> list : bucketList) {
for (double element : list) {
sortedArray[index] = element;
index++;
}
}
return sortedArray;
}
public static void main(String[] args) {
double[] array = new double[]{12, 421, 23, 0, 123, 122, 12, 9};
double[] sortedArray = bucketSort(array);
System.out.println(Arrays.toString(sortedArray)); // [0.0, 9.0, 12.0, 12.0, 23.0, 122.0, 123.0, 421.0]
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
在上述代码中,所有的桶都保存在ArrayList集合中,每一个桶都被定义成一个链表(LinkedList<Double>),这样便于在尾部插入元素。
同时,上述代码使用了JDK的集合工具类Collections.sort来为桶内部的元素进行排序。Collections.sort底层采用的是归并排序或Timsort。
# 七:选择排序
每一轮选出最小元素直接交换到左侧的思路,就是选择排序。这种排序的最大优势,就是省去了多余的元素交换。
下面用数组排序演示一下选择排序的过程。紫色方块代表数组的有序区:
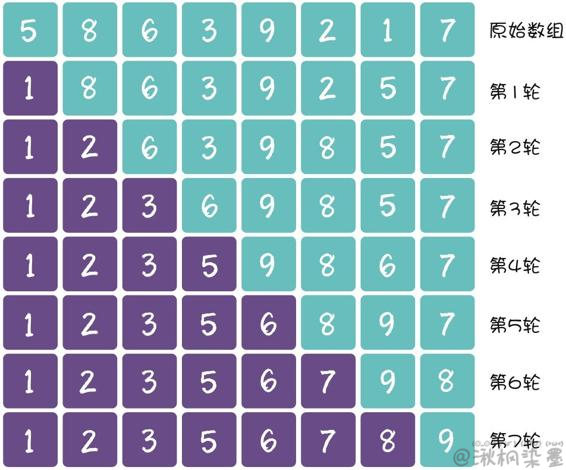
代码实现:
public class SelectSort {
public static void selectionSort(int[] array) {
for (int i = 0; i < array.length - 1; i++) {
int minIndex = i;
for (int j = i + 1; j < array.length; j++) {
if (array[j] < array[minIndex]) {
minIndex = j;
}
}
if (i != minIndex) {
int temp = array[i];
array[i] = array[minIndex];
array[minIndex] = temp;
}
}
}
public static void main(String[] args) {
int[] array = new int[]{3, 4, 2, 1, 5, 6, 7, 8, 30, 50, 1, 33, -4, 7, 0};
selectionSort(array);
System.out.println(Arrays.toString(array));
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
Q:选择排序是不是可以完全取代冒泡排序?
选择排序有一个缺点,就是它的不稳定性。也就是说,当数列包含多个值相等的元素时,选择排序有可能打乱它们原有的顺序。
例如下面这个例子:

上图中,黄色的元素5原本排在橙色的元素5之前,但是随着第1轮元素3和黄色5的交换,使得后续操作中,黄色的元素5排在了橙色的元素5之后。
此外,尽管平均而言冒泡排序的交换次数多于选择排序,但是当数组中的大部分元素有序时,冒泡排序的效率是更高的。
反观选择排序,无论数组元素的有序程度如何,元素交换次数都是n-1次。
# 八:插入排序
维护一个有序区,把元素一个个插入有序区的适当位置,直到所有元素都有序为止。这样的排序算法,被称为插入排序。
下面演示一下插入排序的具体步骤:
给定无序数组如下:

把数组的首元素5作为有序区,此时有序区只有这一个元素:

第1轮
让元素8和有序区的元素依次比较。
8>5,所以元素8和元素5无须交换。
此时有序区的元素增加到两个:

第2轮
让元素6和有序区的元素依次比较。
6<8,所以把元素6和元素8进行交换:

6>5,所以元素6和元素5无须交换。
此时有序区的元素增加到3个:

第3轮
让元素3和有序区的元素依次比较。
3<8,所以把元素3和元素8进行交换:

3<6,所以把元素3和元素6进行交换:

3<5,所以把元素3和元素5进行交换:

此时有序区的元素增加到4个:

以此类推,插入排序一共会进行(数组长度-1)轮,每一轮的结果如下:

代码实现:
public class InsertSort {
public static void insertSort(int[] array) {
for (int i = 1; i < array.length; i++) {
int insertValue = array[i];
int j = i - 1;
// 从右向左比较元素的同时,进行元素复制
for (; (j >= 0) && (insertValue < array[j]); j--) {
array[j + 1] = array[j];
}
// insertValue的值插入适当位置
array[j + 1] = insertValue;
}
}
public static void main(String[] args) {
int[] array = {12, 1, 3, 46, 5, 0, -3, 12, 35, 16}; // [-3, 0, 1, 3, 5, 12, 12, 16, 35, 46]
insertSort(array);
System.out.println(Arrays.toString(array));
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# 九:希尔排序
# 十:归并排序
# 十一:基数排序
# 十二:小结
| 排序算法 | 时间复杂度 | 空间复杂度 | 是否稳定排序 |
|---|---|---|---|
| 冒泡排序 | O(n2) | O(1) | 稳定 |
| 鸡尾酒排序 | O(n2) | O(1) | 稳定 |
| 选择排序 | O(n2) | O(1) | 不稳定 |
| 插入排序 | O(n2) | O(1) | 稳定 |
| 希尔排序 | Sedgewick增量:O(n4/3) | O(1) | 不稳定 |
| 快速排序 | 平均:O(nlogn) 最坏:O(n2) | O(logn) | 不稳定 |
| 堆排序 | O(nlogn) | O(1) | 不稳定 |
| 归并排序 | O(nlogn) | O(n) | 稳定 |
| 计数排序 | O(n+m) | O(m) | 稳定 |
| 桶排序 | O(n) | O(n) | 稳定 |
| 基数排序 | O(k(n+m)) | O(n+m) | 稳定 |
# 十三:参考文献
- 《大话数据结构 — 程杰》
- 《漫画算法 — 魏梦舒》
